Chapter1

1 什么是键？

在第1页和第2页，我们简要回顾了化学键的物理基础。这段讨论不会出现在考试中，因为它不在麦克默里（McMurry）的教材中。它在这里的目的是引入这样一个原理：如果分子采用具有离域（分散）电子分布的几何构型，其能量会更低。麦克默里在课文的几个地方讨论了这一点，尤其是在具有π键的分子中。

1916年，G. N. Lewis提出，键是由两个原子共享的电子对形成，使得两个原子都遵守八隅体规则。键最初用两个点或一条线表示。如今，键用线表示，而路易斯点则用于表示孤对电子（非键合电子对）。

H₂和水的路易斯结构：

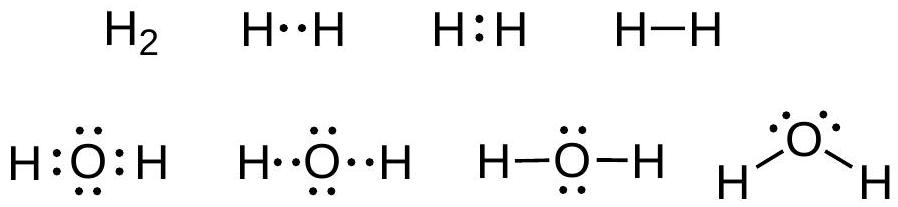
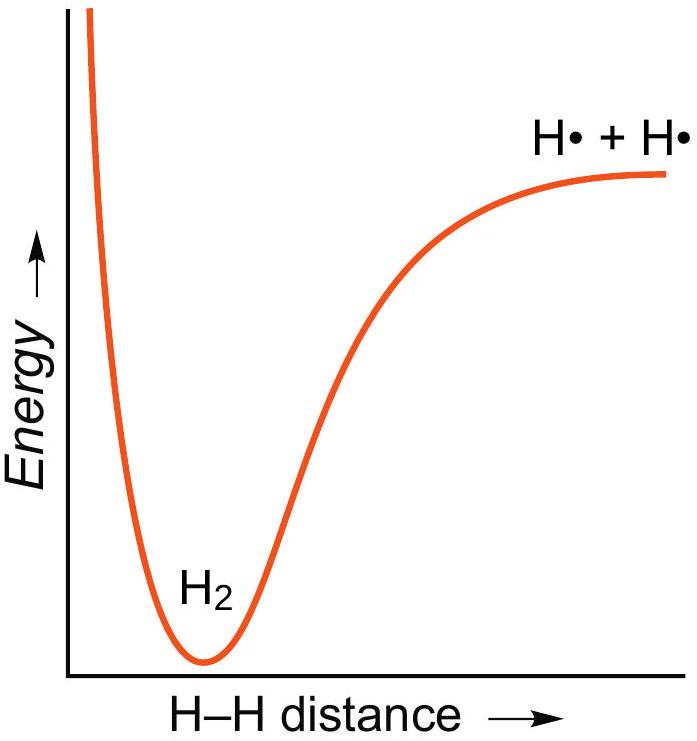
共价键是一种量子现象——它没有经典类比。考虑H₂中的H-H键。当两个H原子相互靠近，它们的1s轨道重叠时，就形成了键。这意味着当原子核靠近（但不过于靠近）时，能量会更低，如右侧图所示。这种能量的降低就是键。H-H键并非连接H原子的独立物理实体，它仅仅是能量-距离曲线右侧的低能量区域。

但什么使能量更低呢？

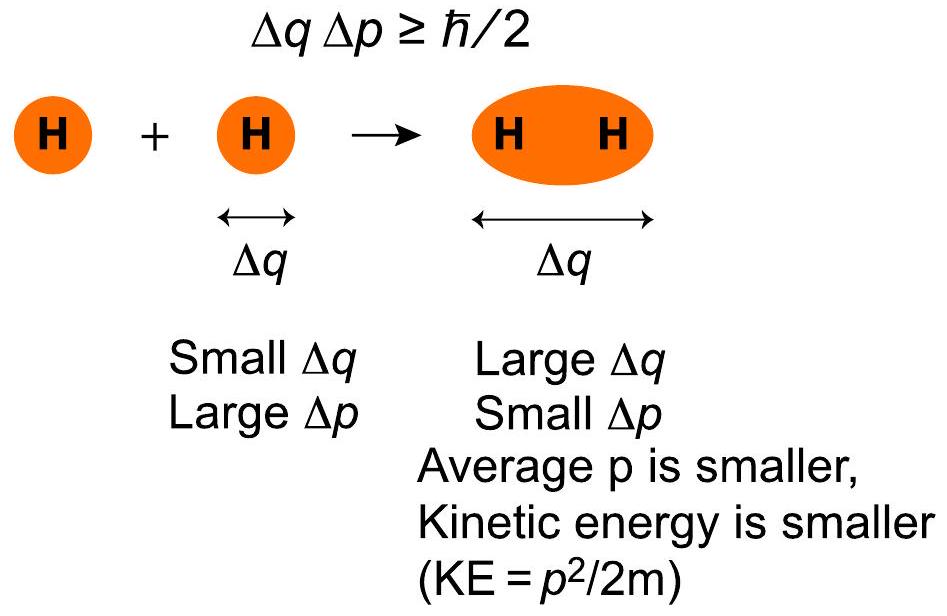
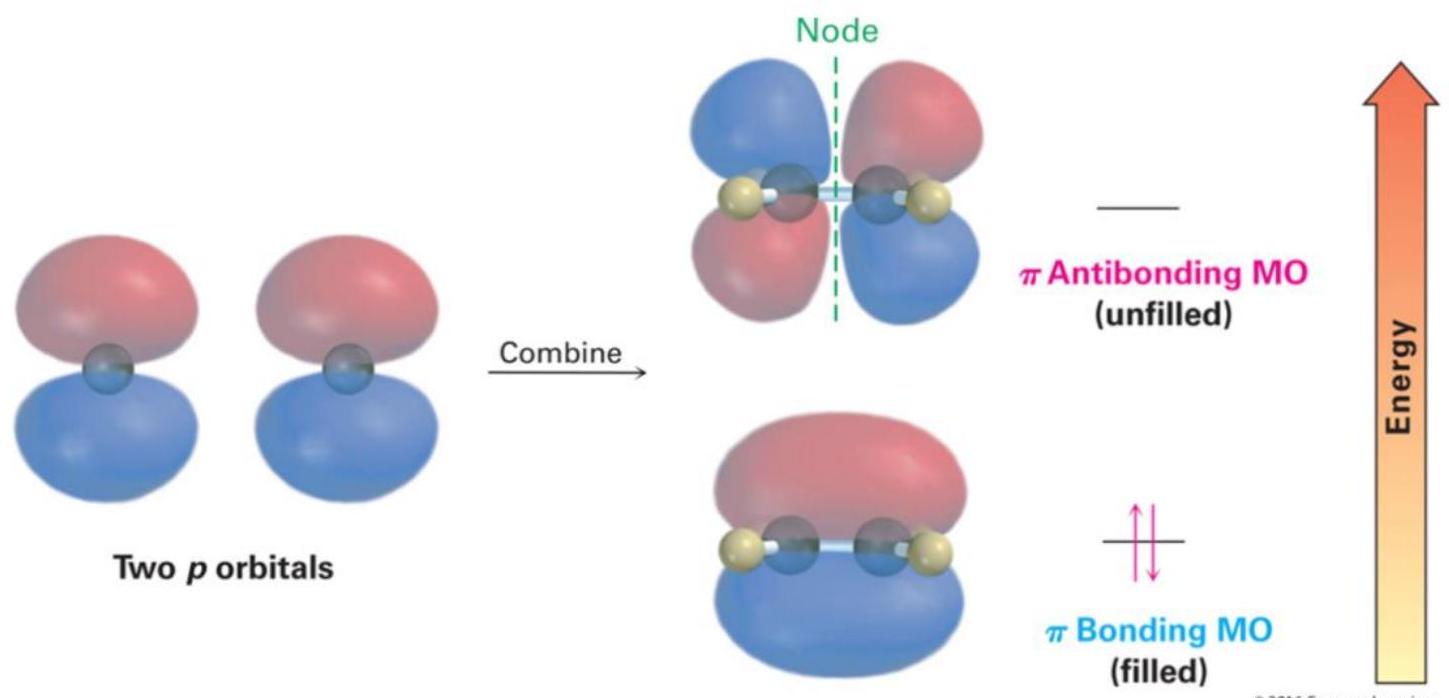
经典和量子效应共同作用，使键合区域的能量降低。库仑定律给出了带电粒子之间的经典静电力（同性相斥，异性相吸）。形成共价键需要两种量子效应。其一是海森堡不确定性原理，$\Delta q \Delta p \geq \hbar / 2$，其中$\Delta q$是电子密度的空间范围（电子位置的不确定性），$\Delta p$是电子动量的范围，$\hbar$是普朗克常数除以$2\pi$。电子运动的空间大小（$\Delta q$，橙色区域）在H₂中比在H原子中更大。这意味着$\Delta p$在H₂中比在H原子中更小。键的形成创造了一个平均电子动量$p$更低的空间。这降低了电子动能（$=p^2 / 2m$）。因此，分子倾向于采用电子密度离域（分散）的几何构型，因为形成低能量分子的概率高于形成异构高能量分子的概率。

另一个对键合很重要的量子效应是泡利不相容原理，它指出原子或分子中没有两个电子可以拥有相同的量子数集。例如，如果两个电子占据同一个空间轨道，它们必须具有相反的自旋。由于电子波函数的这一限制，电子可以占据所有成键分子轨道，而不仅仅是最低能量的轨道。因此，分子可以采用特定的形状，并且块状物质可以占据空间体积。

2 八隅体规则Octet Rule：一个分子只有在每个原子共享8个价电子时才是稳定的。

给定分子式，可以使用八隅体规则推断分子的键连接方式。

在排列键和孤对电子以满足八隅体规则时，请遵循以下电子计数指南：

• 对于一个键，每个原子共享该电子对。两个电子都是每个原子八隅体的一部分。
• 孤对电子的两个电子都被分配给一个单一原子。

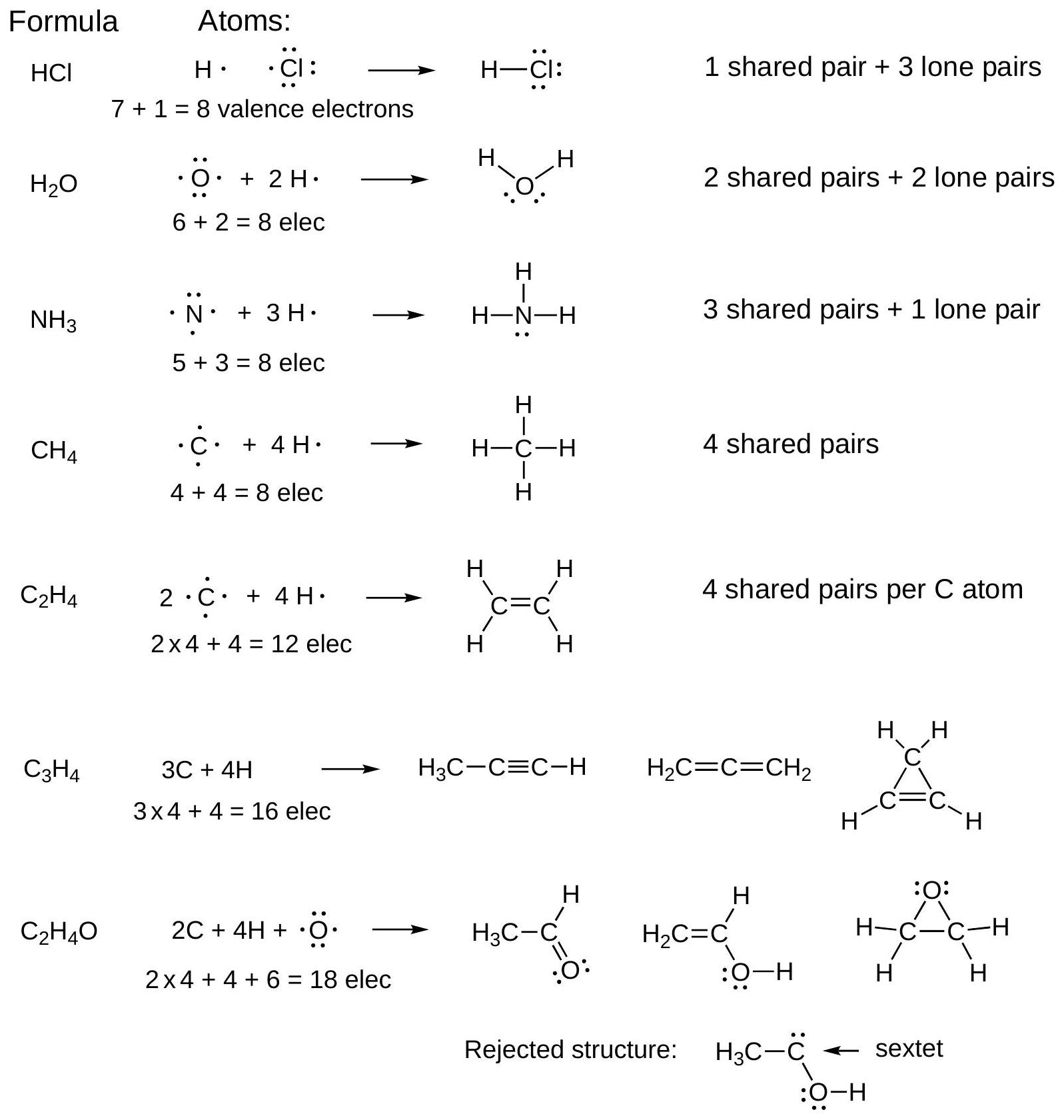
原子轨道

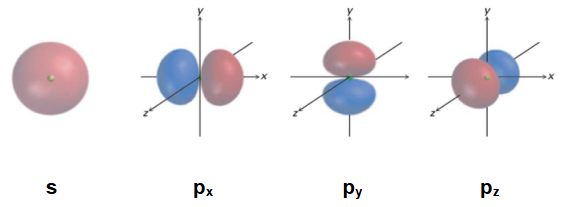
C、N原子基态

3 3-D 分子几何结构和杂化

杂化解决了以下问题： 如果我们知道分子的几何构型，如何理解其键合bonding？ 键合需要相邻原子轨道（AOs）的重叠。 杂化产生单向原子轨道，以实现更有效的键合。

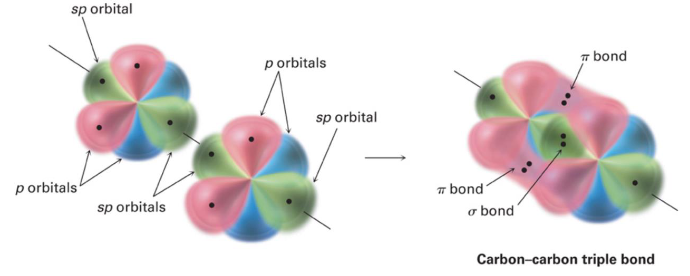
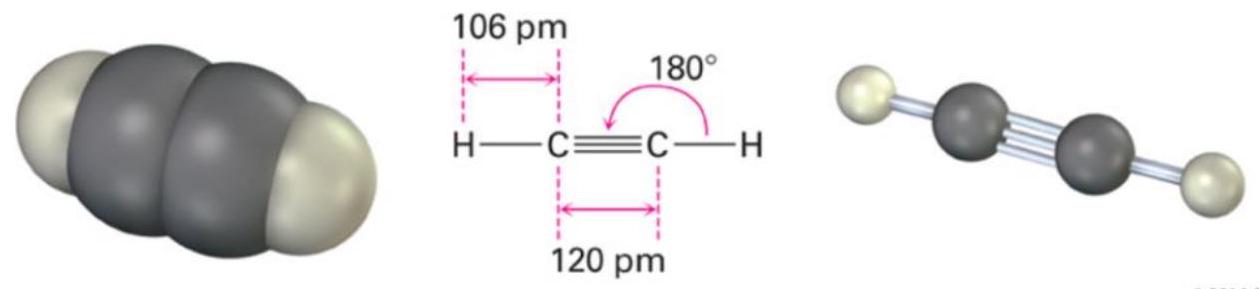
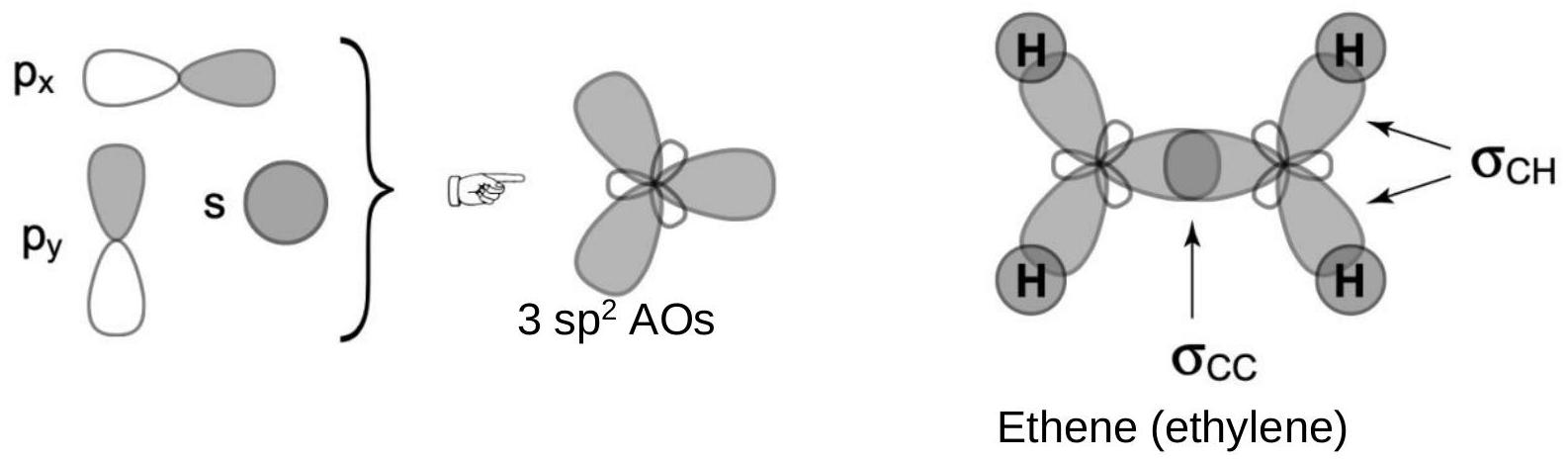
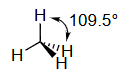
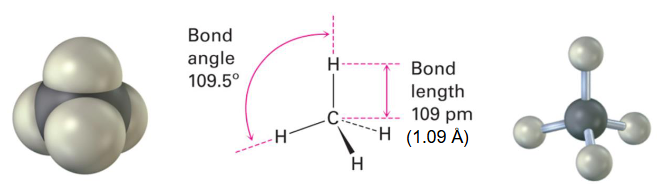
	线性（乙炔） acetylene	平面（乙烯） ethylene	非平面（甲烷） methane
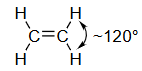杂化: Hybridization	sp	$\mathrm{sp}^{2}$	$\mathrm{sp}^{3}$
s特征: s-character	50%	33%	25%

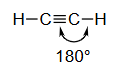
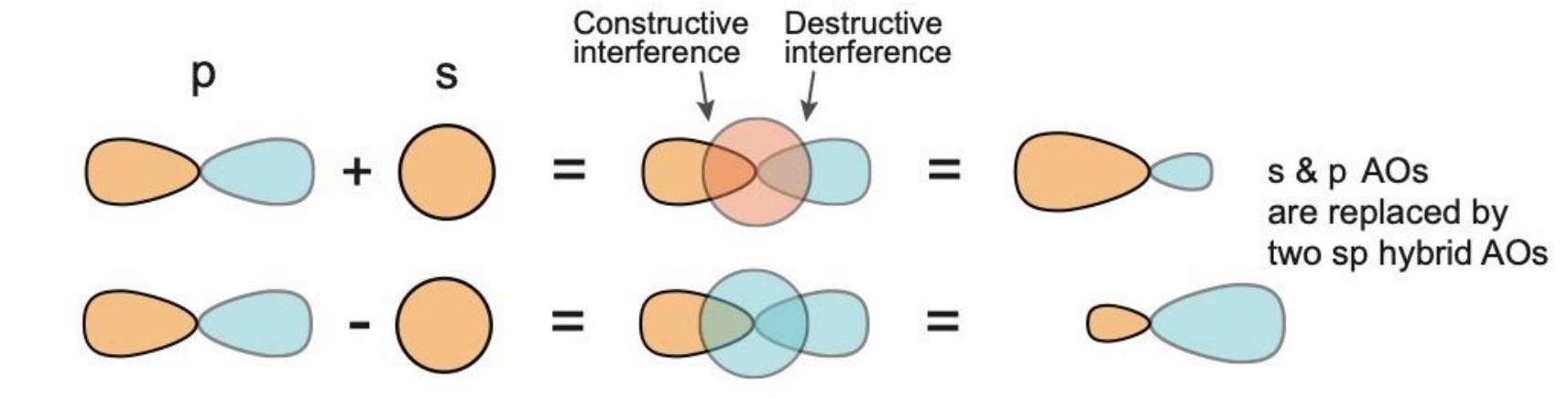
为了在x轴上形成具有180°键角的乙炔，每个碳原子需要一个p_x原子轨道与一个s原子轨道混合（sp杂化），如下图所示。s和p_x原子轨道混合，形成一对沿x轴指向相反方向（180°键角）的sp杂化原子轨道。

sp

在每个碳原子上，s和p原子轨道混合形成一对sp杂化原子轨道：

$\mathrm{sp}^{2}$

碳的s、p_x和p_y原子轨道结合形成3个在x-y平面上的sp²原子轨道。

侧视图

俯视图

$\pi$轨道垂直于sp$^2$ $\sigma$骨架

$\mathrm{sp}^{3}$

碳的s、p_x、p_y、p_z原子轨道结合形成四个具有四面体对称性的sp³杂化原子轨道。

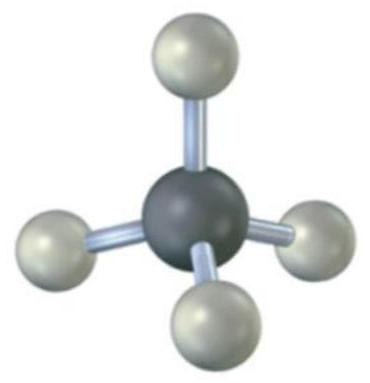
4 根据键连接bond connectivity方式预测杂化hybridization

4.1 计算与一个原子相连的原子数量 + 孤对电子数量

sp³ 原子数量 + 孤对电子数量 = 4 sp² 原子数量 + 孤对电子数量 = 3 sp 原子数量 + 孤对电子数量 = 2

4.2 每个杂化原子都与一个键角相关联，这是一个可测量量。杂化仅对连接到$\geq 2$个其他原子的原子明确定义，这定义了一个键角。

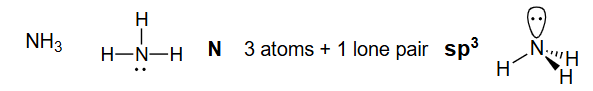
$\mathrm{NH}_{3}$ N 3个原子 +1个孤对电子 $\mathbf{sp}^{\mathbf{3}}$

$\mathrm{H}_{2} \mathrm{O}$ O 2个原子 + 2个孤对电子 $\mathbf{sp}^{\mathbf{3}}$

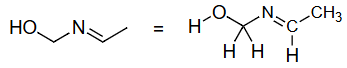
杂化轨道不是唯一定义的（仅限于一个原子）

4.3 具有C、N、O八隅体的常见结构：

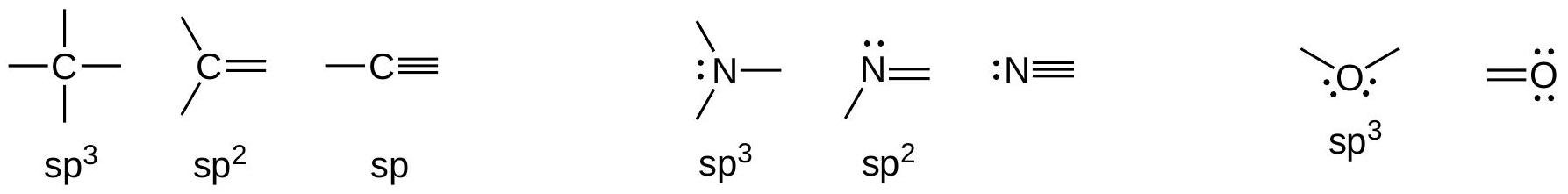
4.4 绘制结构：

如何表示键连接性

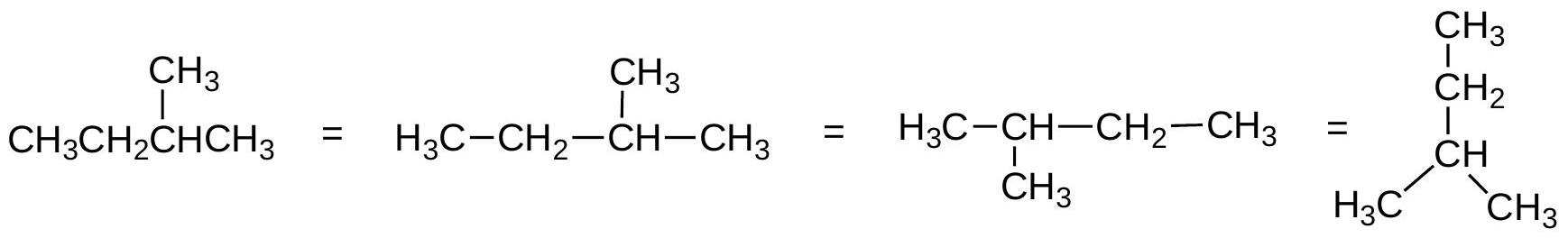
4.5 绘图约定：

• 绘制C-C键，省略C和H标签，除非H连接到杂原子（非碳原子）时才包括H。
• C原子位于拐角处（2个或更多C-C键的交点）和链的末端。
• 连接到C的H原子数量由八隅体规则推断。

上面的分子：

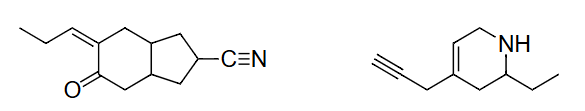
修订上面2个结构，包含每个碳原子上的所有C-H键。